PELUANG : KAIDAH PENCACAHAN
Hallo teman-teman matematika, pada pembahasan kali ini kita akan membahas mengenai kaidah pencacahan nih. Kaidah pencacahan ini merupakan suatu aturan dasar dalam pencacahan dalam kaitannya dengan peluang. Untuk lebih jelasnya silahkan mengikuti pembahasan materi kaidah pencacahan - peluang berikut ini.
KAIDAH PENCACAHAN
Terdapat 3 macam metode dalam kaidah pencacahan yaitu :
Aturan pengisian tempat
Contoh :
1. Tentukan banyaknya cara menyusun kata "SEKOLAH' jika huruf pertama dan terkahirnya harus konsonan
Pembahasan
keterangan
kotak pertama ada 4 pilihan = S,K,L,H
Kotak ketujuh ada 3 pilihan karena tinggal 3 huruf konsonan yang tersisa
Kotak kedua ada 5 pilihan = 3 huruf vocal, 2 kosonan yang tersisa
Kotak ketiga sampe keenam = tinggal sisa dari huruf yang sudah terpakai
2. Tentukan banyaknya bilangan yang terdiri dari 4 angka, yang disusun dari angka-angka 0,1,2,3,4,5 jika
a. angkanya boleh berulang
b. angkanya tidak boleh berulang
Pembahasan
a. boleh berulang
b. angkanya tidak boleh berulang
Permutasi
Permutasi adalah urutan yang mungkin dari sejumlah unsur yang berbeda tanpa adanya pengulangan. Permutasi dapat dirumuskan sebagai berikut.
Contoh:
Hitunglah:
a. P(4,2)
b. P(6,5)
Jawab:
a. =\frac{4!}{(4-2)!}=\frac{4!}{2!}=\frac{4\times&space;3\times&space;2\times&space;1}{2\times&space;1}=12)
b.=\frac{6!}{(6-5)!}=\frac{6!}{1!}=\frac{6\times&space;5\times&space;4\times&space;3\times&space;2\times&space;1}{1}=720)
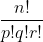
b.
- Permutasi dengan beberapa elemen sama
Contoh:
Tentukan banyaknya kata yang terdiri atas 5 huruf yang disusun dari 2 huruf A, 1 huruf B, 1 huruf S, dan 1 huruf I.
Jawab:
Banyaknya kata yang dapat disusun adalah

- Permutasi Siklis
Permutasi siklis dari objek n adalah !) cara
cara
Contoh:
Lima orang siswa sedang membaca di sebuah meja bundar. Berapa banyak cara agar kelima siswa tersebut dapat duduk secara melingkar dengan urutan yang berbeda?
Jawab:
Banyaknya cara agar kelima siswa tersebut dapat duduk secara melingkar dengan urutan yang berbeda adalah (5-1)! = 4! = 4 x 3 x 2 x 1 = 24 cara
Contoh:
Lima orang siswa sedang membaca di sebuah meja bundar. Berapa banyak cara agar kelima siswa tersebut dapat duduk secara melingkar dengan urutan yang berbeda?
Jawab:
Banyaknya cara agar kelima siswa tersebut dapat duduk secara melingkar dengan urutan yang berbeda adalah (5-1)! = 4! = 4 x 3 x 2 x 1 = 24 cara
Kombinasi
Kombinasi adalah suatu teknik yang menyatakan banyaknya cara dalam menyusun beberapa objek dari suatu grup tanpa memperhatikan urutan. Kombinasi dinotasikan dengan C(n,k) atau
Contoh:
Hitunglah!
a. C(6,3)
b. C(4,2)
Jawab:
a. =\frac{6!}{(6-3)!3!}=\frac{6!}{3!3!}=\frac{6\times&space;5\times&space;4\times&space;3\times&space;2\times&space;1}{3\times&space;2\times&space;1\times&space;3\times&space;2\times&space;1}=20)
b.=\frac{4!}{(4-2)!2!}=\frac{4!}{2!2!}=\frac{4\times&space;3\times&space;2\times&space;1}{2\times&space;1\times&space;2\times&space;1}=6)
b.
Faktorial
Definisi: n faktorial dinotasikan dengan n! dan didefinisikan sebagai perkalian berikut.
Contoh:
Hitunglah:
a. 3!
b. 
Jawab:
a. 3! = 3 x 2 x 1 = 6
b.
Jawab:
a. 3! = 3 x 2 x 1 = 6
b.
Teman-teman itu dia materi singkat mengenai kaidah pencacahan. Untuk lebih memahami materi tersebut, kami menyediakan beberapa tipe soal dan pembahasannya nih. Yuk simak bersamaan!
Soal dan Pembahasan
1. Jika tersedia 3 kursi dan terdapat 3 orang yang akan menduduki kursi-kursi tersebut maka banyaknya susunan yang mungkin terjadi adalah ... cara
Pembahasan
=\frac{3!}{(3-3)!})

2. Terdapat 7 orang yang dicalonkan untuk menjadi ketua RW, sekretaris, dan bendahara. Banyaknya susunan yang dapat terjadi dalam pencalonan tersebut adalah...
Pembahasan
3. Di dalam sebuah perkumpulan, terdapat 20 orang yang belum saling kenal. Jika kedua puluh orang tersebut akan bersalaman satu sama lain sebanyak dua kali, banyaknya salaman yang dapat terjadi adalah...
Pembahasan
4. Di dalam sebuah tes, setiap siswa diminta mengerjakan 10 dari 15 soal dengan syarat soal-soal nomor ganjil harus dikerjakan. Banyak pilihan soal yang dapat dikerjakan siswa tersebut adalah...
Pembahasan
Soal-soal nomor ganjil yang harus dikerjakan 8 soal yaitu nomor {1, 3, 5, 7, 9, 11, 13, 15}
Jadi, siswa dapat memilih 2 dari 7 soal yang tersisa, yaitu
5. Pada suatu rapat dihadiri oleh 6 orang yang duudk mengelilingi sebuah meja bundar. Berapa banyak susunan duduk yang dapat terjadi?
Pembahasan
P = (n-1)! = (6-1)! = 5! = 5 x 4 x 3 x 2 x 1 = 120
Jadi, banyaknya susunan duduk yang dapat terjadi ada 120 cara

0 Response to "PELUANG : KAIDAH PENCACAHAN"
Post a Comment