Menentukan Penyelesaian Sistem Persamaan Linear Dua Variabel dengan Metode Substitusi
Simak materi berikut dengan baik!
Sistem persamaan linear dua variabel adalah sebuah sistem dari dua atau lebih persamaan linear dua variabel yang sejenis. Untuk menyelesaikan sistem persamaan linear dua variabel terdapat beberapa cara atau metode yang bisa dilakukan, satu diantaranya akan kita bahas kali ini yaitu metode substitusi.
Metode substitusi adalah metode atau cara yang digunakan untuk menyelesaikan sebuah sistem persamaan linear dua variabel dengan mensubstitusikan (mengganti) variabel dengan persamaan yang baru.
Adapun langkah-langkah yang perlu dilakukan diantaranya, perhatikan contoh berikut.
Diketahui
tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel tesebut!
Langkah 1: Pilihlah salah satu persamaan (pilih yang paling sederhana jika ada), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x
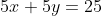... persamaan (1)
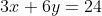... persamaan (2)
Dari dua persamaan, misal dipilih persamaan (2), sehingga
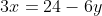
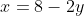... persamaan (3)
Langkah 2: Substitusikan nilai x atau y (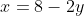) yang didapat pada persamaan yang belum dipilih, sehingga
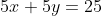
+5y=25 "5(8-2y)+5y=25")
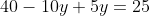
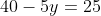
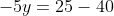
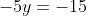
Langkah 3: Substitusikan nilai x atau y yang dihasilkan pada langkah 2 ke persamaan (3), sehingga
 "x=8-2(3)")
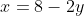
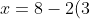Jadi, himpunan penyelesaian dari SPLDV di atas dapat ditulis (x,y) = (2,3)
Mudah bukan metode ini? untuk menambah pemahaman kalian, coba perhatikan beberapa soal dan pembahasan berikut.
Soal dan Pembahasan
Diketahui sistem persamaan
. Tentukan nilai x.y !
Pembahasan
Langkah 1: Pilihlah salah satu persamaan (pilih yang paling sederhana jika ada), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x
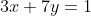... persamaan (1)
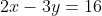... persamaan (2)
Misal dipilih persamaan (1), sehingga
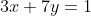
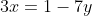
... persamaan (3)
Langkah 2: Substitusikan nilai x atau y dari pers (3) pada persamaan yang belum dipilih, sehingga
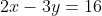
-3y=16 "2(\frac{1-7y}{3})-3y=16")
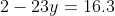
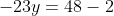
Langkah 3: Substitusikan nilai x atau y yang dihasilkan pada langkah 2 ke persamaan (3), sehingga
}{3} "x=\frac{1-7(-2)}{3}")
Jadi, himpunan penyelesaian dari SPLDV di atas dapat ditulis (x,y) = (5,-2)
Sistem persamaan linear dua variabel adalah sebuah sistem dari dua atau lebih persamaan linear dua variabel yang sejenis. Untuk menyelesaikan sistem persamaan linear dua variabel terdapat beberapa cara atau metode yang bisa dilakukan, satu diantaranya akan kita bahas kali ini yaitu metode substitusi.
Metode substitusi adalah metode atau cara yang digunakan untuk menyelesaikan sebuah sistem persamaan linear dua variabel dengan mensubstitusikan (mengganti) variabel dengan persamaan yang baru.
Adapun langkah-langkah yang perlu dilakukan diantaranya, perhatikan contoh berikut.
Diketahui
Langkah 1: Pilihlah salah satu persamaan (pilih yang paling sederhana jika ada), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x
Dari dua persamaan, misal dipilih persamaan (2), sehingga
Langkah 2: Substitusikan nilai x atau y (
Langkah 3: Substitusikan nilai x atau y yang dihasilkan pada langkah 2 ke persamaan (3), sehingga
Jadi, himpunan penyelesaian dari SPLDV di atas dapat ditulis (x,y) = (2,3)
Mudah bukan metode ini? untuk menambah pemahaman kalian, coba perhatikan beberapa soal dan pembahasan berikut.
Soal dan Pembahasan
Diketahui sistem persamaan
Pembahasan
Langkah 1: Pilihlah salah satu persamaan (pilih yang paling sederhana jika ada), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x
Misal dipilih persamaan (1), sehingga
Langkah 2: Substitusikan nilai x atau y dari pers (3) pada persamaan yang belum dipilih, sehingga
Langkah 3: Substitusikan nilai x atau y yang dihasilkan pada langkah 2 ke persamaan (3), sehingga
Jadi, himpunan penyelesaian dari SPLDV di atas dapat ditulis (x,y) = (5,-2)
0 Response to "Menentukan Penyelesaian Sistem Persamaan Linear Dua Variabel dengan Metode Substitusi"
Post a Comment