TRANSFORMASI GEOMETRI
Simaklah materi berikut ini dengan baik!
Transformasi adalah pemetaan suatu titik pada suatu bidang ke himpuna titik pada bidang yang sama. Ada 4 jenis transformasi yang bisa dilakukan pada suatu titik, yaitu:
1. Translasi (Pergeseran)
\overset{T(a,b)}{\rightarrow}A'(x+a,y+b))
Contoh:
Tentukan bayangan dari titik A (2, 3) oleh translasi T = (7, 8) !
Jawab:
\overset{T(7,8)}{\rightarrow}A'(2+7,3+8))
\overset{T(7,8)}{\rightarrow}A'(9,11))
Jadi bayangan titik A (2,3) adalah A' (9,11)
2. Refleksi (Pencerminan)
\overset{C(0,0)}{\rightarrow}A'(-x,-y))
\overset{M=x}{\rightarrow}A'(x,-y))
\overset{M=y}{\rightarrow}A'(-x,y))
\overset{M_{y=x}}{\rightarrow}A'(y,x))
\overset{M_{y=-x}}{\rightarrow}A'(-y,-x))
\overset{M_{x=k}}{\rightarrow}A'(2k-x,y))
\overset{M_{y=k}}{\rightarrow}A'(x,2k-y))
Contoh:
Tentukan bayangan dari titik B(2,-3), jika dicerminkan terhadap:
a. sumbu x
b. garis y=x
Jawab:
a.\overset{M=x}{\rightarrow}B'(x,-y))
\overset{M=x}{\rightarrow}B'(2,3))
b.\overset{M_{y=x}}{\rightarrow}B'(y,x))
\overset{M_{y=x}}{\rightarrow}B'(-3,2))
3. Rotasi (Perputaran)
Rotasi atau perputaran merupakan perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu yang berlawanan arah dengan jarum jam. Adapun sifat dari rotasi "bangun yang diputar (rotasi) tidak mengalami perubahan bentuk dan ukura". Rotasi dapat dirumuskan sebagai berikut:
\overset{R(P(p,q),\alpha&space;)}{\rightarrow}A'(x'y'))


Contoh:
Titik B) diputar dengan arah berlawanan jarum jam sejauh 45° menghasilkan titik B'. Tentukan koordinat dari titik B!
diputar dengan arah berlawanan jarum jam sejauh 45° menghasilkan titik B'. Tentukan koordinat dari titik B!
Jawab:
Rotasi sebuah titik dengan sudut sebesar α


&&space;-1/2\sqrt{2}(9\sqrt{2})\\&space;1/2\sqrt{2}(5\sqrt{2})&&space;1/2\sqrt{2}(9\sqrt{2})&space;\end{pmatrix})


4. Dilatasi (Perkalian dengan Skalar)
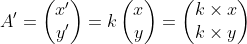
+a\\&space;k(y-b)+b&space;\end{pmatrix})
Contoh:
Tentukan bayangan titik A(8, 2) oleh dilatasi [O, 1/2]!
Jawab:
Diketahui. titik A(8,2), pusat (0,0) dan skala = 1/2

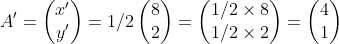
Oke, itu tadi pembahasan mengenai rumus pada transformasi geometri yang terdiri dari translasi, refleksi, rotasi, dan dilatasi, Semoga bermanfaat :) Silahkan simak ulasan mengenai soal latihan dan pembahasannya berikut.
SOAL DAN PEMBAHASAN
Tentukan bayangan garis 2x – y = 5 apabila dicerminkan terhadap sumbu x!
Pembahasan
\overset{M=x}{\rightarrow}A'(x,-y))
sehingga, x=x dan y= -y maka
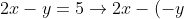=5)
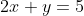
jadi bayangannya adalah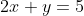
Tentukan bayangan garis y = 3x – 5 oleh translasi T (-2, 1)!
Pembasahan
\overset{T(a,b)}{\rightarrow}A'(x+a,y+b))
sehingga, substitusikan x=x'+2 dan y=y'-1 maka
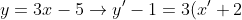-5)


Jadi bayangan nya adalah
Contoh soal dan pembahasan
1. Titik A (-4,1) di translasikan oleh . Koordinat bayangan titik A adalah ....
. Koordinat bayangan titik A adalah ....
A.)
B.)
C.)
D.)
E.)
Penjabaran
Inget translasi itu artinya pergeseran bisa dengan cara dijumlahan atau dengan cara dikurangi tergantung angka yang terdapat disoal
Ketika mempunyai titik awal A (-4,1) kemudian ditrasnlasikan oleh , maka kita menghitungnya dengan cara
, maka kita menghitungnya dengan cara
)
)
Transformasi adalah pemetaan suatu titik pada suatu bidang ke himpuna titik pada bidang yang sama. Ada 4 jenis transformasi yang bisa dilakukan pada suatu titik, yaitu:
1. Translasi (Pergeseran)
Translasi adalah perpindahan atau pergeseran suatu titik sehingga mendapat suatu titik yang baru (bayangan dari titik semula). Adapun sifat dari translasi "bangun yang digeser (translasi) tidak mengalami perubahan bentuk dan ukuran". Translasi dapat dirumuskan sebagai berikut:
Titik A(x,y) ditranslasikan oleh T(a,b) menghasilkan bayangan A'(x',y') dituliskan dengan
Contoh:
Tentukan bayangan dari titik A (2, 3) oleh translasi T = (7, 8) !
Jawab:
Jadi bayangan titik A (2,3) adalah A' (9,11)
2. Refleksi (Pencerminan)
Refleksi adalah pencerminan suatu titik terhadap suatu garis yang menghasilkan bayangan dari titik tersebut. Adapun sifat dari refleksi " bangun yang dicerminkan (refleksi) dengan cermin datar tidak mengalami perubahan bentuk dan ukuran. Jarak bangun dengan cermin (cermin datar) adalah sama dengan jarak bayangan dengan cermin tersebut". Refleksi dapat dirumuskan sebagai berikut:
- Pencerminan terhadap titik C(0,0)
- Pencerminan terhadap sumbu x
- Pencerminan terhadap sumbu y
- Pencerminan terhadap garis y=x
- Pencerminan terhadap garis y=-x
- Pencerminan terhadap garis x=k
- Pencerminan terhadap garis y=k
Contoh:
Tentukan bayangan dari titik B(2,-3), jika dicerminkan terhadap:
a. sumbu x
b. garis y=x
Jawab:
a.
b.
3. Rotasi (Perputaran)
Rotasi atau perputaran merupakan perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu yang berlawanan arah dengan jarum jam. Adapun sifat dari rotasi "bangun yang diputar (rotasi) tidak mengalami perubahan bentuk dan ukura". Rotasi dapat dirumuskan sebagai berikut:
- Rotasi dengan pusat P(p,q) dan sudut
- Rotasi dengan pusat O(0,0) daan sudut
Contoh:
Titik B
Jawab:
Rotasi sebuah titik dengan sudut sebesar α
4. Dilatasi (Perkalian dengan Skalar)
Dilatasi adalah perbesaran atau pengecilan suatu objek sehingga ukuran benda dapat menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi faktor pengalinya. Dilatasi dapat dirumuskan sebagi berikut:
- Dilatasi titik A(x,y) terhadap pusat O(0,0) dengan faktor skala k
- Dilatasi titik A(x,y) terhadap pusat P(a,b) dengan faktor skala k
Contoh:
Tentukan bayangan titik A(8, 2) oleh dilatasi [O, 1/2]!
Jawab:
Diketahui. titik A(8,2), pusat (0,0) dan skala = 1/2
Oke, itu tadi pembahasan mengenai rumus pada transformasi geometri yang terdiri dari translasi, refleksi, rotasi, dan dilatasi, Semoga bermanfaat :) Silahkan simak ulasan mengenai soal latihan dan pembahasannya berikut.
SOAL DAN PEMBAHASAN
Tentukan bayangan garis 2x – y = 5 apabila dicerminkan terhadap sumbu x!
Pembahasan
sehingga, x=x dan y= -y maka
jadi bayangannya adalah
Tentukan bayangan garis y = 3x – 5 oleh translasi T (-2, 1)!
Pembasahan
sehingga, substitusikan x=x'+2 dan y=y'-1 maka
Jadi bayangan nya adalah
Contoh soal dan pembahasan
1. Titik A (-4,1) di translasikan oleh
A.
B.
C.
D.
E.
Penjabaran
Inget translasi itu artinya pergeseran bisa dengan cara dijumlahan atau dengan cara dikurangi tergantung angka yang terdapat disoal
Ketika mempunyai titik awal A (-4,1) kemudian ditrasnlasikan oleh
0 Response to "TRANSFORMASI GEOMETRI"
Post a Comment